Menghitung Fuzzy C-Means (FCM)
Hallloo kembali lagi disini :p kali ini saya akan sharing tentang bagimana Menghitung Fuzzy C-Means (FCM) sesuai langkah-langkahnya. Sebagai bahan referensi yang saya gunakan adalah proceeding dari seorang peneliti yang bernama Lin Ma dengan judul "Using Fuzzy C -Means And Fuzzy Integrals For Machinery Fault Diagnosis" dengan judul proceeding "International Conference on Condition Monitoring, Cambridge, England" tahun 2005 dan tambahan dari sumber yang lainnya. Baik kita mulai saja,Algoritma FCM dapat diimplementasikan dalam langkah-langkah berikut ini [13]:
1. Masukan data yang akan diklaster X , berupa matriks berukuran n x m (n=jumlah sampel data, m = atribut setiap data). Xik = data sampel ke-i (i=1,2,...,n), atribut ke-k ( k =1,2,...,m).
2. Menentukan:
- Jumlah cluster = c
- Pangkat = w
- Maksimum Iterasi = MaxIter
- Error terkecil yang diharapkan = ξ(Epsilon)
- Fungsi objectif awal = P0 = 0
- Iterasi awal = t = 1
3. Membangkitkan bilangan random μik, i=1,2,3 ..., n; k=1,2,3 ...c; sebagai elemen-elemen matriks partisi awal U.
Menghitung jumlah tiap kolom:
..............(2.14)
dengan j=1,2,…n
Menghitung:
..............(2.15)
4. Menghitung pusat vektor tiap-tiap klaster untuk matrik partisi tersebut sebagai berikut:
.............(2.16)
5. Menghitung fungsi objectif pada iterasi ke-t:
.............(2.17)
6. Menghitung perubahan matriks partisi:
.............(2.18)
dengan: i=1,2,…n; dan k=1,2,….c
7. Mengecek kondisi untuk berhenti, yaitu:
- Jika ( | Pt-Pt-1 | < ξ) atau(t > MaxIter) maka berhenti
- Jika tidak: t=t+1, mengulang langkah ke-4.
Sekian dulu kalau ada kesempatan saya akan memberikan contohnya terima kasih :)
- Inisialisasi matrix keanggotaan
- Menghitung cluster centroids
- Menghitung fungsi generalized loss
- Menghitung hasil ambang batas Proses berulang terus menerus sampai kondisi terminate terpenuhi.
1. Masukan data yang akan diklaster X , berupa matriks berukuran n x m (n=jumlah sampel data, m = atribut setiap data). Xik = data sampel ke-i (i=1,2,...,n), atribut ke-k ( k =1,2,...,m).
2. Menentukan:
- Jumlah cluster = c
- Pangkat = w
- Maksimum Iterasi = MaxIter
- Error terkecil yang diharapkan = ξ(Epsilon)
- Fungsi objectif awal = P0 = 0
- Iterasi awal = t = 1
3. Membangkitkan bilangan random μik, i=1,2,3 ..., n; k=1,2,3 ...c; sebagai elemen-elemen matriks partisi awal U.
Menghitung jumlah tiap kolom:
..............(2.14)
dengan j=1,2,…n
Menghitung:
..............(2.15)
4. Menghitung pusat vektor tiap-tiap klaster untuk matrik partisi tersebut sebagai berikut:
.............(2.16)
5. Menghitung fungsi objectif pada iterasi ke-t:
.............(2.17)
6. Menghitung perubahan matriks partisi:
.............(2.18)
dengan: i=1,2,…n; dan k=1,2,….c
7. Mengecek kondisi untuk berhenti, yaitu:
- Jika ( | Pt-Pt-1 | < ξ) atau(t > MaxIter) maka berhenti
- Jika tidak: t=t+1, mengulang langkah ke-4.
Sekian dulu kalau ada kesempatan saya akan memberikan contohnya terima kasih :)
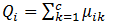





Komentar
Posting Komentar
Silahkan Berkomentar Dengan Sopan ya.. :)
Jika Anda PUNYA HALAMAN WEB gunakanlah pilihan 'Name/URL' pada pilihan 'Beri Komentar Sebagai'.
Jika anda TIDAK PUNYA Account Blog gunakanlah pilihan 'Anonymous' pada pilihan 'Beri Komentar Sebagai'.